Convolutions and Neural Networks

In my last blog post, I took you by the hand and guided you through the realm of convolutions. I hope to have made it clear why it makes sense to discretize functions and represent them as vector, and how to calculate the convolution of 1D and 2D vectors.

In this post I want to talk a little about how Image Processing was done in the old times, and show the relation between the procedures performed back then and the kinds of parameters learnt by Convolutional Neural Networks (CNN). In fact, do notice that CNNs have been lurking around for years (LeNet had been introduced in 1998!) before they went viral again in 2012 (with the AlexNet), so, in a way, they are concurrent models to the models described below.

It is hard to tell why Convolutional Neural Networks took so long to become popular. One reason might be that Neural Networks had gone somewhat out of fashion for a while until their revival some years ago. (Hugo Larochelle commented in this TEDx video how there were papers that were rejected simply based on the argument that his approach used Neural Networks.)

Another contributing factor might be that, for a long time, it was a common belief for many people that Neural Networks with many layers were not good (despite the work with LSTMs being done in Europe). They were taken as “hard to train” and empirically many experiments ended up producing better performances for models with just a few (or even only one) layer. CNNs, however, did not suffer from these problems (at least not that much), and the LeNet paper from 1998 had already 5 layers.

But my focus here is not on the architecture of CNNs, nor on their gradient flow or their history. My focus here is on how exactly we can say that the shared weights of a CNN results in a mathematical formulation that is identical to that of the Convolutions that we discussed in the previous post.

Image Processing

Before I go into the CNNs I want to show why a Convolutional is something that we might want to do to an image. In my previous post, I tried to be as generic as possible, talking about functions and vectors, speaking from a “signal processing” point of view. It turns out that the Image Processing community has its own perspective. So, from now on, I will take $f$ as a 2D image that I want to somehow process, and to $g$ as a kernel.

When we learn math in school, we learn names of several functions that are known to be useful, and somehow represent well parts of the world we live in. Examples of such functions are $log$, $ln$, $sin$, or $tg$. When we are introduced to statistics, we get acquainted to several other names, such as “correlation”, “standard deviation”, “variance”, “mean” or “mode”. The types of kernels used in Image Processing are not different: researchers in the area have found through the years several kernels that are known to perform well different kinds of tasks, such as blurring, edge detection, sharpening, etc. You can find a list of such kernels in the Wikipedia article.

I want to show how a convolution could be used to find the edges of an image. But this time, I don’t want to show formulas; I think some Python code should make things clearer. Let’s say we want to find the borders of the following image of Lenna:

The first thing to do is to load the image:

from PIL import Image
img = Image.open('lenna.bmp')

Then I want to create a function to convolve the image with the kernel:

# import numpy as np

def convolve(image, kernel):
	# Flips the kernel both left-to-right and up-to-down
	kernel = np.fliplr(np.flipud(kernel))

	# Transforms the image into something that numpy can process
	image_array = np.array(image)

	# Initializes the image I want to return
	new_image_array = np.zeros(image_array.shape)

	# Convolve
	for i in range(image_array.shape[0] - kernel.shape[0]):
		for j in range(image_array.shape[1] - kernel.shape[1]):
			# run_kernel will perform the pointwise multiplication
			# followed by sum
			new_image_array[i][j] = run_kernel(image_array, kernel, i, j)

	# Creates a new Image object
	new_image = Image.fromarray(new_image_array)

	# Returns both the image as an array, and as an Image object
	return new_image_array, new_image

As you can see, I am using numpy to perform the calculations. I expect you not to find it hard to understand the code. It could obviously be written much more efficiently (numpy actually even has a function that performs the convolution anyway), but I wanted to show how the operations we saw in the last blog post can be easily translated into some piece of code.

Now we need to define that run_kernel() function. It calculates the $\odot$ operation between the part of the image that we are interested in and the (already flipped) kernel. This is as simple as:

def run_kernel(image, kernel, pos_x, pos_y):
	ret = 0
	for i in range(kernel.shape[0]):
		for j in range(kernel.shape[1]):
			ret += image[pos_x + i][pos_y + j] * kernel[i][j]

	return ret

Done! It is that simple!

What we are missing is just the right kernel. If you look at the Wikipedia page you’ll see that there are several kernels usable for Edge detection. I’ll use the third one:

In Python:

new_image_array, new_image = convolve(img, np.array([[-1,-1,-1],[-1,8,-1],[-1,-1,-1]]))
new_image.show()

With this, you should see the following image:

Nice, right?

The Border Problem

If you look carefully at this new image, you’ll see that I’m not running run_kernel() in the last pixels (and then you’ll find some columns of zero pixels at the right of the image, as well as some some rows at the bottom). This has to do with what I called the “Border Problem” in my last post.

It is actually very unclear what should be done in the edges of the Image we are trying to process. The way I have been doing so far, if I calculate a convolution between two $3 \times 3$ matrices, it will give me only one number. If you think well about what the size of the final output would be, you will see that it depends on the kernel size. Let’s assume that our final image has $n$ pixels both horizontally and vertically. For a kernel of size $1 \times 1$ (i.e., just a number), the size of the final image would be the same as the size of the original image If the kernel were $2 \times 2$, then the output would have size $n-1 \times n-1$. For a $3 \times 3$ kernel, it would be $n-2 \times n-2$. You can see how this generalizes to $n-(k+1) \times n-(k+1)$, where $k$ is the size of the kernel.

It would be nice if I could find ways to get a result that had the same size of the input image. The most obvious way to do this is to assume that there are zeros beyond the borders of the images. If you think that the images are signals just like the signals from my previous blog post, you should feel that this is a very reasonable assumption to make. Using this assumptions, you will see three types of convolutions:

• Valid: This is the way I have been doing it so far. We don’t assume any information apart from what we have.

• Full: This is the case where we assume there are lots of zeros beyond that the edge of the original image. This way, if we were given the image $f$ below, then it would be “transformed” into the $f_{transformed}$ below before convolving. The number of new rows/columns introduced depends on the size of the kernel. As I said, this should make sense from the perspective of signal processing I described in my previous post. (if this is not clear enough, you are welcome to take a look at this amazing explanation I found in Stack Overflow)

• Same: This is a little trickier. It also assume zeros around the image, but only as much as needed to return an output that has the exact same size as the input image. I tend to find it hard to visualize, but I found that this image helped a lot.

Relation to Convolutional Neural Networks

Ok… so I think we covered everything there was to cover about Convolutions. Now I just need to answer: how do they relate to CNNs?

Remember how the convolutions are being calculated: for a given point in “time”, we multiply the values of both matrices pointwise and then sum them all. Now… remember how the connections of the Convolutional Layer are organized:

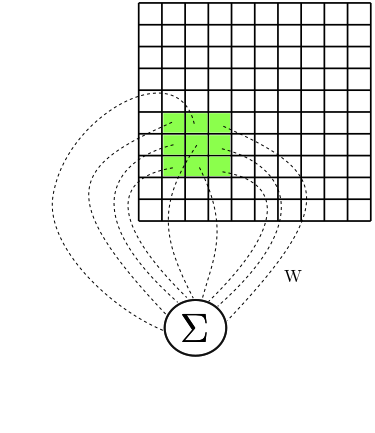
Let’s look at one neuron individually. I’d like to call it $a$. It has access to a certain rectangular part of the image. Let’s represent the values of this rectangular part by $A$. So, for example, $A_{0,0}$ represents the element in the leftmost and topmost corner of that rectangular part of the image that our neuron $a$ has access to.

Now, let’s say that $W$ is a matrix with the weights corresponding to the connections between $a$ and the values in $A$. Then the input to $a$ is calculated as

Doesn’t this look a lot like the $\odot$ operation from our kernels? It looks a lot like I am running run_kernel() giving as input the subimage $A$ and the kernel $W$.

Now, let’s focus on another neuron, $b$, and again use a new matrix $B$ to represent the rectangular part of the image that our second neuron has access to. (I hope you see where this is going.) Again, let $V$ denote a matrix composed of the weights of the connections between $b$ and $B$. Then, again, the input to $b$ is calculated as

Again, it looks a lot like I just calculated $B \odot V$, doesn’t it?

If this is hard to see with the formulas, the following image should help a little. It shows the subimages $A$ and $B$, and the connections $W$ and $V$, and how the values are summed when given as input to our neurons $a$ and $b$:

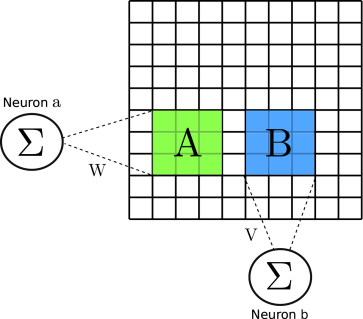
Ok, so now you know that the Convolutional layer is running our $\odot$ operation on small subparts of the image. There is just one last point to be made: Convolutional Neural Networks use shared weights. This means the $W = V$! And this also means that the kernel $W$ (or $V$) is always the same for whichever neuron you choose. This means that if I chose at random any new neuron $c$ to inspect (and defined $C$ as the matrix corresponding to the rectangular part of the input image that $c$ has access to), then the calculation that I would perform would still be

(because, as I said $W = V$!)

In summary, this means that the operation these layers are performing is identical to a Convolution!

Why do we want CNNs?

Now you could ask me: ok, the Image Processing community knows all of these kernels that do magic with my images. Why would I care to have a complex architecture that ends up doing exactly the same kind of thing?

The answer I am going to give is simple, but has huge implications. So far, the Image Processing community had to use their knowledge about how real images generally look like and burn a lot of their own neurons (I mean, figuratively) to generate kernels that somehow fit the problems they were trying to solve. So, if they wanted to find characteristics in the images that would help them to solve the problem they were trying to solve, they had to manually invent kernels that they deemed useful for their task. Many of these kernels followed some patterns/constraints of, e.g., summing up to 1, so that the values of the output image wouldn’t saturate. These patterns somehow limited the types kernels that one could invent, and it was very unintuitive to create anything following different patterns.

But what if, instead of creating kernels by hand (and being bound by constraints, and by our intuition) we could just give a lot of data to a statistical model and just hope that it learns something useful in the end? This is exactly what Convolutional Neural Networks are for. The kernels that are learnt by the CNN are generally not very intuitive, and probably no human would have easily guessed that they are useful for the tasks that these networks are trying to solve (be it classification, of segmentation, or whatever). Still, they have shown great results, and (I would go so far as to say that) the times of “handcrafted feature engineering” are probably over.

Bonus: Shifting a Signal

Before concluding this blog post, I want to show how convolutions can be unexpectedly useful to perform some seemingly unrelated task: the shifting of a signal. I learnt this in the Neural Turing Machines paper and found it a very elegant way of solving the problem. In this section, I’ll go back to my old notation and refer to the 1D signal $f$. Let’s say it is a discrete signals represented by the following vector:

Now let’s say I want to shift all elements of $f$ to the right. How would I do? One way to do it could be to make a “same” convolution of $f$ with a function $g = [1,0,0]$. Let’s see how this would work.

(here, I am taking $t=0$ is when the first element of $f$ is aligned with the element in the center of $g$)

And what if I wanted to shift it to the left? Just use a different function $g = [0, 0, 1]$:

This example should also give an intuition of how convolutions are a good way of processing signals. In the case of the Neural Turing Machines, instead of shifting the signals so “binarily” to the right or to the left, they allow continuous values to the positions of $g$. For example, $g$ could be anything like $[0.8, 0.1, 0.1]$. In that case, most of the signal would be shifted, but part of the information would remain “spread” (“blurred”) through other positions of the signal. While this may be unintuitive, we have seen how unintuitive things may actually be useful for solving some tasks.

Conclusion

I hope to have given a good notion of how CNNs relate to the convolutions we saw in the previous post. My hope is that this will provide a good intuition for how convolutions can be used for other Machine Learning architectures, and allow you to think of convolutions as just some other tool that you can use to solve your problems. As you can see, all of this is very simple, but I wish someone had shown me these ideas when I started learning, instead of having to learn them all by myself. I hope this post makes it easy to extend architectures based on convolutions in a way that is sensible taking into account everything discussed here.