What are Convolutions?
12 Aug 2017For quite some time already I have been wanting to write this blog post. A little more than one year ago I got acquainted to Convolutional Neural Networks, and it didn’t immediately strike me why they are called that way. I eventually read this blog post that helped a lot to clarify things; but I thought I could try to give more details on what exactly is meant when one says “Convolution” here.
This blog post builds upon the description given there, so, if you still didn’t read that, stop reading this and go there take a look at that blog post. I may overlap some of the discussions here with the discussions there.
In the sections that follow, I’ll introduce convolutions (actually, I’ll let Kahn Academy do that for me), then introduce a procedure to calculate it, motivate a discussion about discrete convolutions, show why it makes sense to represent the convolving functions as vectors and extend the definition to the 2D space. The next blog post will explain why these are useful for signal processing and what is their relation with Convolutional Neural Networks.
Convolutions
Convolutions are a very common operation in signal processing. While the colah’s blog post presents it in a more abstract/intuitive statistical way, I find that a more gore calculus-driven introduction from Kahn Academy might help you realize that the concept is just an integral:
In this Kahn Academy video, Sal found a closed formula for the convolution by solving the integral. Given that a convolution is an integral, you might consider that it represents the area below some curve. But what curve exactly? I’ll discuss more about it in the next section. For now, what is worth is to understand that there several ways in which you can think of convolutions, and it might help a lot if you allow yourself to switch views at different points in time.
A concrete example
If you go to the Wikipedia article on convolutions, you may find the following two (awesome) images:
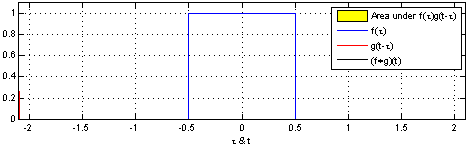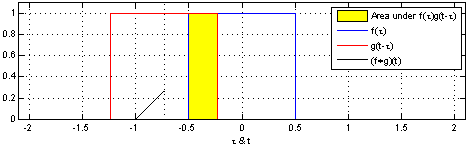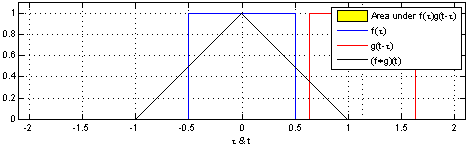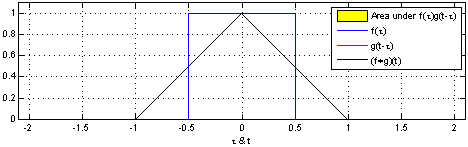
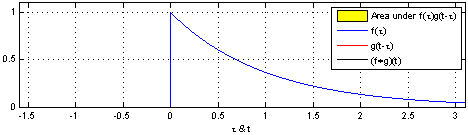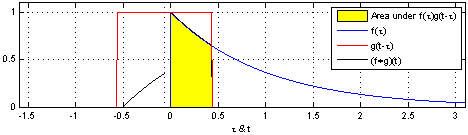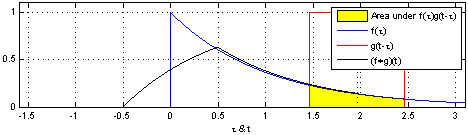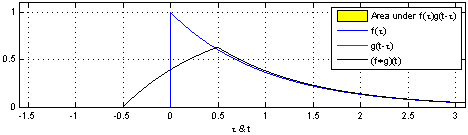
What these images are saying is that you can calculate the value of the convolution $f \ast g$ at the point $t$ by following a very simple procedure. I’ll define two functions $f$ and $g$ to make the steps easier to follow. Let
\[f(x) = \begin{cases} 1 & \text{if } 0 \leq x \leq 1 \\ 0 & \text{otherwise} \end{cases}\]and
\[g(x) = 2 \times f(x)\]Here we have the two curves:
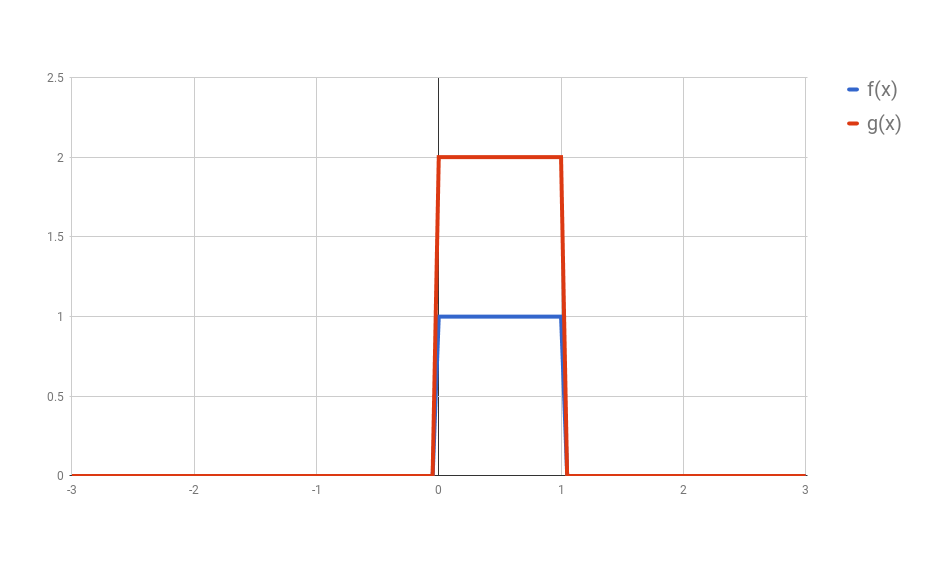
(I used Google Spreadsheets to do this, so you’ll notice the lines are not exact, but you should be able to get the idea)
First: flip $g$ horizontally (i.e., $g(x) <- g(-x)$). Let’s give the flipped $g$ a name, say $g’$. (if you don’t flip $g$, then what you are calculating has actually the name of “cross-correlation”, and is simply another typical operation in signal processing.).
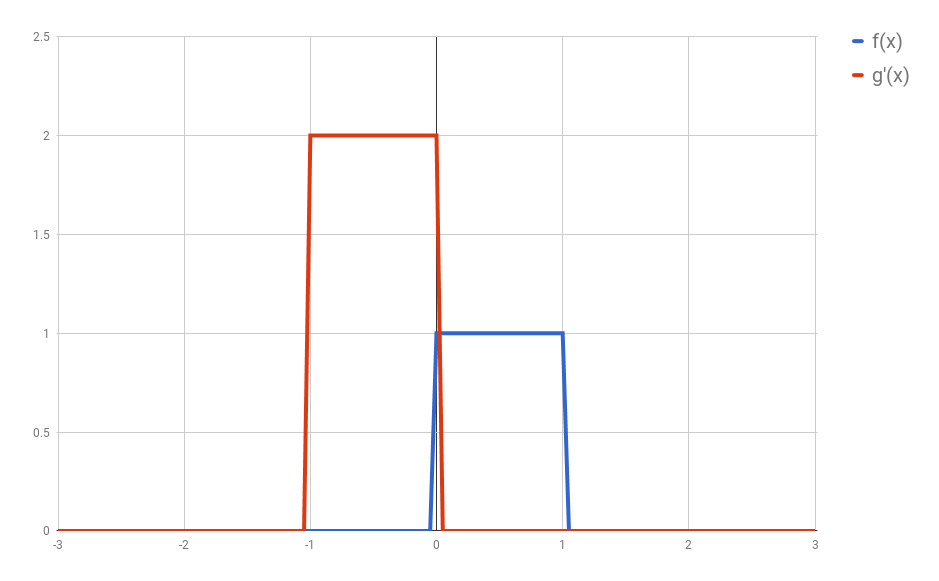
Second: shift $g’$ horizontally by $t$ units. If $t$ is positive, then $g’$ will be shifted to the right; otherwise, it will be shifted to the left. For our example, let’s say that $t=0.3$. I’ll call this function $g_{shifted}’$
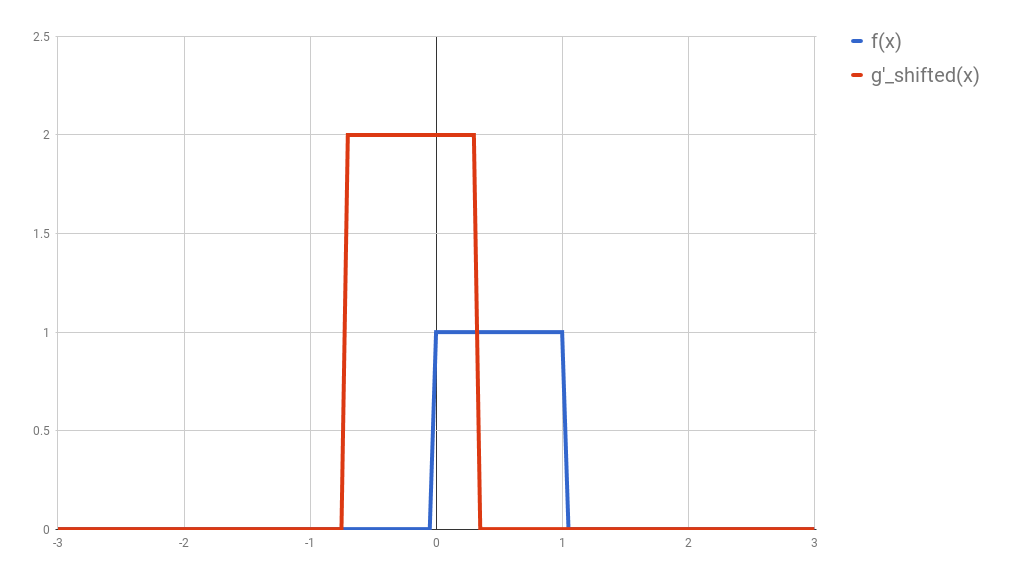
Third: this is the step where the problems arise. Now what you want is actually multiply the two curves are each point between $-\infty$ and $+\infty$ and calculate the area below the curve that this multiplication will form. Let’s assume that the functions are zero most of the time (just like in our example), and non-zero only in a small section of their domain. Because we are multiplying the two values, we only care about the values where both functions are not 0. In all other cases, the integral will be 0 anyway. Let’s assume that both functions are non-zero only in an interval $[a, b]$. In this case, our problem reduces to calculating the integral of the multiplication of $f$ and $g_{shifted}’$ inside that interval. Now it could still be a challenge to calculate the integral of the $g_{shifted}’$ and “f” in that interval.
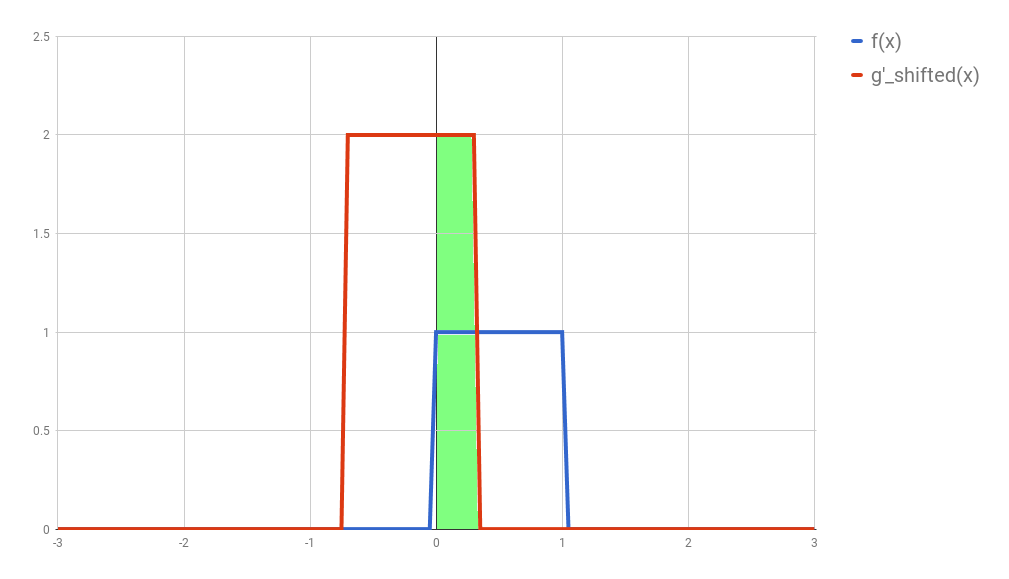
(While searching for a way to understand this procedure, I came across this very nice demo. In it you can define your own functions and play arround to find out how the convolution is going to be.)
The problem with continuous convolutions is that we would have to actually calculate an integral. But what if our function were actually “discrete”? Fortunately for us, most applications on Image Processing require discrete signals, and for our purposes it would be perfectly ok to discretize these continuous signals.
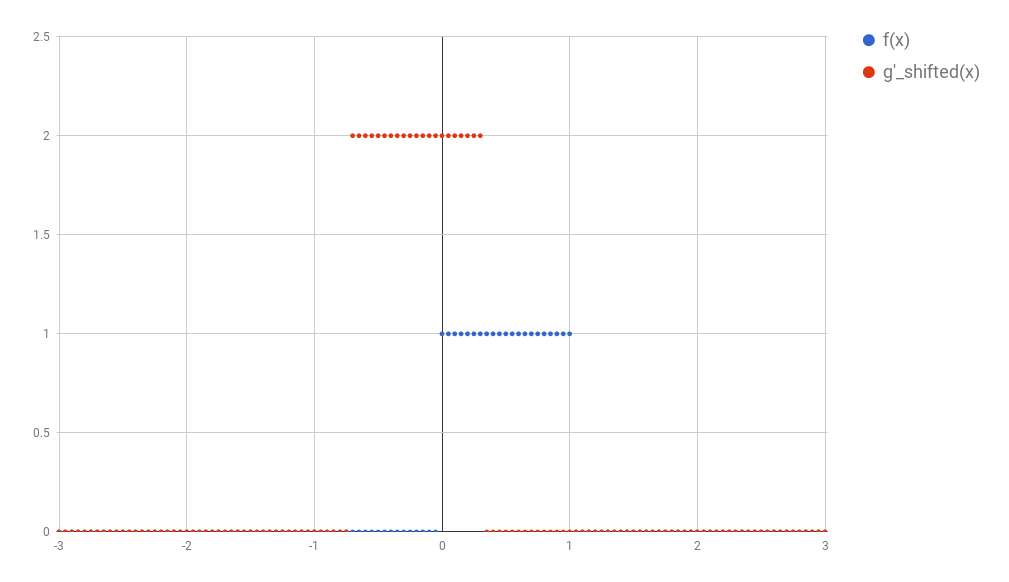
After discretization, All the concepts we have discussed so far would follow the same logic. Now, instead of an integral we now have a sum. So, given the interval $[a, b]$, we could calculate the convolution as
\[(f \ast g)(t) = \sum^b_{i=a}{f(i) \times g_{shifted}'(i)}\]And fortunately this sum is easy to calculate.
Note: the avid reader may notice that the integral of an interval spanning only a point should have been 0 (and therefore the convolution should always have become 0 after the discretization). The reason why this does not work has to do with the dirac delta function, and I won’t go into many details here. You can just assume that the discretized version of the signal is a sum of dirac delta functions.
In the example above I discretized the functions using 1 point for each 0.05 step in $x$. This would make the discussion below very hard to understand. So, to make things simpler, in all the text that follows I’ll use steps of 0.25 instead. The image below shows how the original functions $f$ and $g$ would look like discretized this way.
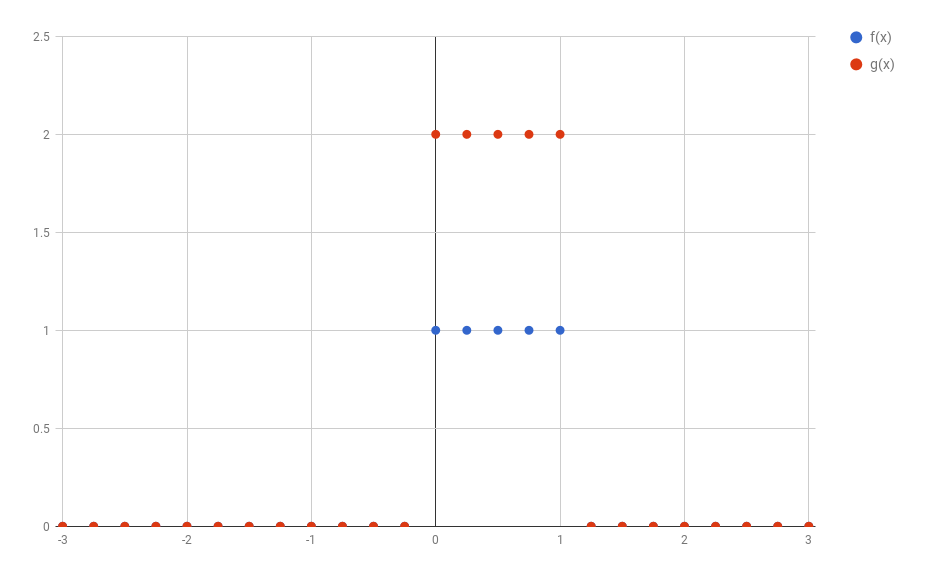
1D discrete convolutions
It turns out that the functions $f$ and $g$ used in convolutions are in reality most of the times composed almost entirely by zeros (as assumed before). This allows for a much more compact representation of the functions as a vector of values. For example, $f$ and $g$ could be represented as:
\(f = [\dots 0, 0, 1, 1, 1, 1, 0, 0, \dots] \\ g = [\dots 0, 0, 2, 2, 2, 2, 0, 0, \dots] \\\) (Of course, the number of 1 and 2 depends on how the discretization was performed)
Now let’s say I’d like to calculate the value of the convolution between $f$ and $g$ at the point $t = $some coordinate. It is hard to point the exact place, so I’ll make the place bold:
\(f = [\dots 0, 0, 1, 1, \textbf{1}, 1, 0, 0, \dots] \\\) (For future reference, I’ll call this position $t=2$)
The way to calculate it is just the same:
-
Flip $g$ (but it has no effect here, because $g$ is symmetric anyway);
-
Move $g$ horizontally by $t$: this is a little abstract here; but if we align the $f$ and $g$ the way they were initially aligned, then we should get:
- Multiply all elements position by position and sum them all.
You might have noticed how these operations may resemble dot-products. You could have implemented them as:
\[(f \ast g)(t) = [1, 1] \bullet [2, 2]\]This way, if you wanted to calculate the convolution for many different values of $t$, you could just keep shifting the vector $g$.
\[\begin{align*} \text{When } t &= 0 \\ f &= [\dots 0, 0, \textbf{1}, \textbf{1}, \textbf{1}, \textbf{1}, 0, \dots] \\ g &= [\dots 0, 0, \textbf{2}, \textbf{2}, \textbf{2}, \textbf{2}, 0, \dots] \\ (f \ast g)(t) &= [1, 1, 1, 1] \bullet [2, 2, 2, 2] = 8 \\ \\ \text{When } t &= 1 \\ f &= [\dots 0, 0, 1, \textbf{1}, \textbf{1}, \textbf{1}, 0, 0, \dots] \\ g &= [\dots 0, 0, 0, \textbf{2}, \textbf{2}, \textbf{2}, 2, 0, \dots] \\ (f \ast g)(t) &= [1, 1, 1] \bullet [2, 2, 2] = 6 \\ \\ \text{And, } & \text{finally, if you consider all values of } t \\ f &= [\dots 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, \dots] \\ g &= [\dots 0, 0, 0, 0, 2, 2, 2, 2, 0, 0, \dots] \\ (f \ast g)(t) &= [\dots 0, 2, 4, 6, 8, 6, 4, 2, 0, 0, \dots] \\ \end{align*}\]Unfortunately, these are still vectors with an infinite number of dimensions, which are hard to store in our limited storage computers. It is worth noting that very often the functions $f$ and $g$ for which we want to calculate a convolution are 0 most of the time. Since we know that the result of the convolution in these regions will be zero, we can just drop all of the zeros:
\(\begin{align*} f &= [0, 0, 0, 0, 1, 1, 1, 1, 0, 0] \\ g &= [0, 0, 0, 0, 2, 2, 2, 2, 0, 0] \\ (f \ast g) &= [0, 2, 4, 6, 8, 6, 4, 2, 0, 0] \\ \end{align*}\) (As you can see, I kept some of the zeros. I could have removed them. It was my choice)
And congratulations, we just arrived in a very compact representation of our functions.
Note: The entire discussion so far supposed that we would keep $f$ still and always transform $g$ according to our three steps to calculate the convolutions. It turns out that convolutions are commutative, and therefore the entire procedure would have also worked by holding $g$ still and changing $f$ in the same way. (Incidentally, they are also associative)
But what does all of this mean?
When I started talking about convolutions, I said that they are used a lot in the context of signal processing. It might be a good idea to forget that these vectors are functions for a while and consider them signals. (this video might help to convince you that this is a sensible idea.) In that case, what a convolution is doing is taking two signals as input and generating a new one based on those two. How the new signal looks like depends on where both signals are non-zero. In the next blog post you’ll see how this can be used in meaningful ways, like finding borders in an image, blurring an image, or even shifting a signal in a certain direction.
Most importantly, convolutions are a very simple operation (composed of sums and multiplications that can be done parallely), which can be easily implemented in hardware. They are a great tool to have in hand when solving difficult problems.
2D Convolutions
It shouldn’t be a big leap to extend these concepts to the 2D space.
Let us skip all the discussion about continuous functions and vectors with infinitely many elements and consider our current state: functions $f$ and $g$ are represented as small vectors, and we want to calculate the convolution of those two functions (vectors) at any point $t$. If we now define new $f$ and $g$ in a 2D space, then we can represent them as matrices. For example, if we now redefine $f$ as
\[f(x, y) = \begin{cases} 1 & \text{if } 0 \leq x,y \leq 1 \\ 0 & \text{otherwise} \end{cases}\]and rediscretize it in the same way we did before, then we would get a matrix that looks something like:
\[f = \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 & 1 & 0 \\ 0 & 1 & 1 & 1 & 1 & 0 \\ 0 & 1 & 1 & 1 & 1 & 0 \\ 0 & 1 & 1 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix}\](Do not forget: I was the one who decided to keep a border with zeros. I could have left many more columns and rows with zeros in the borders. This may seem irrelevant for now, but will be useful when we discuss kernels in the next blog post.)
Let us define a new $g$, that after discretization looks like the following:
\[g = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0.5 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix}\]How would the convolution then be calculated? Same steps:
-
Flip the matrix $g$ (both horizontally and vertically), generating $g’$.
-
Shift $g’$ (according to the place where you want to evaluate the convolution). Basically, you want to align $g’$ with some part of $f$.
-
Multiply the aligned elements and sum their result.
An example calculated by hand
Before concluding this blog post, I want to calculate an example by hand. If you did not understand everything so far, this should clarify whatever is missing. Let’s define two new functions $f$ and $g$, that, after discretization and “vectorization”, become the following matrices:
\[f = \begin{bmatrix} 0 & 3 & 6 & 3 \\ 3 & 6 & 3 & 6 \\ 6 & 3 & 6 & 3 \\ 3 & 6 & 3 & 0 \\ \end{bmatrix}\] \[g = \begin{bmatrix} 0 & 3 & 0 \\ 0 & 1 & 2 \\ 4 & 0 & 0 \\ \end{bmatrix}\]If you think of $f$ as an image, you might interpret it as two diagonal lines (the values with 6) surrounded by some “shade” (the values with 3). The function $g$, on the other hand, is hard to interpret. I chose a very asymmetric matrix to show how the flipping (the first step in our calculation) affects the final values in $g$.
Let’s calculate $(f \ast g)(0,0)$. First is to flip $g$ to create $g’$:
\[g' = \begin{bmatrix} 0 & 0 & 4 \\ 2 & 1 & 0 \\ 0 & 3 & 0 \\ \end{bmatrix}\]Then we align the matrix $g’$ with the part of $f$ that corresponds to position $(0,0)$. This part might cause some confusion. Where exactly is $(0,0)$? There is no actual “right answer” to where this point should be after discretization, and we don’t have the original function formula to help us find out. I’ll call this “the border problem” and refer to it in the next blog post. For now, I’ll just align with the points “we know” and forget about any zeros that might lurk beyond the border of the matrix representing $f$. This will give us a so-called “valid” convolution.
Finally, we need to multiply each element pointwise and sum all of the results. To make things clearer, if $A$ and $B$ denoted the two matrices of same size that we now have, then what we want to do is:
\[A \odot B = \sum_{i,j}{f_{i,j} \times g_{i,j}}\]Where I am representing this “pointwise multiplication followed by sum” by the operator $\odot$. In our specific case, we get:
\[\begin{split} (f \ast g)(0,0) &= \begin{bmatrix} 0 & 3 & 6 \\ 3 & 6 & 3 \\ 6 & 3 & 6 \\ \end{bmatrix} \odot \begin{bmatrix} 0 & 0 & 4 \\ 2 & 1 & 0 \\ 0 & 3 & 0 \\ \end{bmatrix} \\ &= (0 \times 0) + (3 \times 0) + (6 \times 4) + (3 \times 2) + (6 \times 1) + (3 \times 0) + (6 \times 0) + (3 \times 3) + (6 \times 0) \\ &= 45 \end{split}\]Easy, right?
Now to calculate $(f \ast g)(1,0)$ we just move the matrix $g$ to the right, aligning it with the next submatrix of $f$:
\[\begin{split} (f \ast g)(1,0) &= \begin{bmatrix} 3 & 6 & 3 \\ 6 & 3 & 6 \\ 3 & 6 & 3 \\ \end{bmatrix} \odot \begin{bmatrix} 0 & 0 & 4 \\ 2 & 1 & 0 \\ 0 & 3 & 0 \\ \end{bmatrix} \\ &= (3 \times 0) + (6 \times 0) + (3 \times 4) + (6 \times 2) + (3 \times 1) + (6 \times 0) + (3 \times 0) + (6 \times 3) + (3 \times 0) \\ &= 45 \end{split}\]And the other two elements are calculated the same way:
\[\begin{split} (f \ast g)(0,1) &= \begin{bmatrix} 3 & 6 & 3 \\ 6 & 3 & 6 \\ 3 & 6 & 3 \\ \end{bmatrix} \odot \begin{bmatrix} 0 & 0 & 4 \\ 2 & 1 & 0 \\ 0 & 3 & 0 \\ \end{bmatrix} \\ &= (3 \times 0) + (6 \times 0) + (3 \times 4) + (6 \times 2) + (3 \times 1) + (6 \times 0) + (3 \times 0) + (6 \times 3) + (3 \times 0) \\ &= 45 \end{split}\] \[\begin{split} (f \ast g)(1,1) &= \begin{bmatrix} 6 & 3 & 6 \\ 3 & 6 & 3 \\ 6 & 3 & 0 \\ \end{bmatrix} \odot \begin{bmatrix} 0 & 0 & 4 \\ 2 & 1 & 0 \\ 0 & 3 & 0 \end{bmatrix} \\ &= (6 \times 0) + (3 \times 0) + (6 \times 4) + (3 \times 2) + (6 \times 1) + (3 \times 0) + (6 \times 0) + (3 \times 3) + (0 \times 0) \\ &= 45 \end{split}\]Resulting in the final matrix:
\[(f \ast g) = \begin{bmatrix} 45 & 45 \\ 45 & 45 \\ \end{bmatrix}\]Conclusions
In this blog post I expect to have given you a very intuitive understanding of how convolutions are calculated and a notion of what they are doing. It should help you to make the connection between all those integrals you find in Kahn Academy or Wikipedia and the discrete convolution operation you see in some Neural Networks. If none of this still happened, the examples of the next blog post will definitely help you to realize what is going on.
I had not planned for this blog post to become so long. In the next blog post I’ll show applications of convolutions from the image processing field, and how they connect to Convolutional Neural Networks. As a bonus, I want to show a very elegant application of convolutions from the Neural Turing Machines.
Stay tuned =)
UPDATE: Thanks to Fotini Simistira for pointing some mistakes in my calculations.