A (Very Simple) Introduction to Representation Learning

This blog post is the result of a conversation I had with some friends some time ago. The discussion started when an idea was raised: that the hidden layers of a Neural Network should be called its “memory”. To say the truth, one could think that way, if he wants to think that the network is storing in a “memory” what it has learnt. Still, the way people tend to take it is that these are “latent variables” that the network learnt to extract from the noisy signal that is given to it as input.

This raised the topic of Representation Learning, which I thought I’d discuss a little here. I would like to focus on the task of classification, where a given input must be assigned a certain label $y$. Let’s even simplify things and say that we have a binary classification task, where the label $y$ can be either $0$ or $1$. I’d like to think that I have a dataset $\textbf{x} = {x_1, x_2, x_3, … }$ composed by many inputs $x_i$, where each $x_i$ could be some vector.

Let’s imagine what happens when we start stacking several layers after one another. Even better, let’s see it:

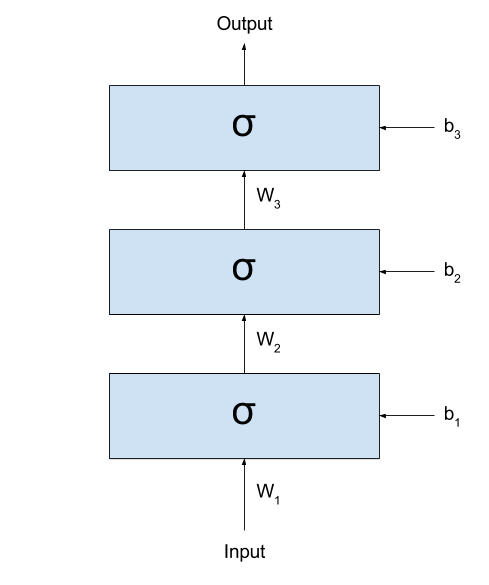
If we call the output of the network $y_{prediction}$, we could represent the same network with the following formula:

(I like a lot to look at these formulas. They demystify a lot all the complexity that Neural Networks seem to be built upon.)

As you can see (and as very well discussed in this great Christopher Olah’s blog post), what these networks are doing is basically

• Linearly transforming the input space into some other space (this is done by the multiplication by $W_k$ and sum by $b_y$);
• Non-linearly transforming the input space through the application of the sigmoid function.

Each time these two steps are applied, the input values are more distinctly separated into two groups: those where $y = 0$, and those where $y = 1$. There is, for most $x_i$ in class $y=0$ and $x_j$ is in class $y=1$, the values in $\sigma(W_1 \times x_i + b_1)$ and $\sigma(W_1 \times x_j + b_1)$ will probably be better separable than the raw $x_i$s and $x_j$s. (here, I am using the expression “better separable” very loosely. I hope you get the idea: the values will not necessarily be “farther” from each other, but it will probably be easier to trace a line dividing all elements of the two classes.)

This way, if I treat the inputs as signals, then the input to the next layer could be thought as a cleaned version of the signal of the previous layer. By cleaned version I mean that the output of the previous (lower) layer are “latent variables” extracted from the (potentially) noisy signal used as input.

To make things clearer, I would like to present an example. Imagine I gave you lots of black and white images with digits written by hand: (these are MNIST images. I am linking to an image from Tensorflow. I hope it won’t change the link so soon =) )

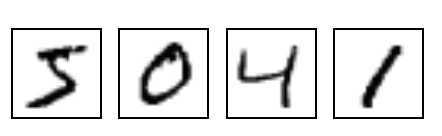
(to keep the binary classification task, let’s say I want to divide them into “smaller than 5” and “not smaller than 5”.)

The first hidden layer would then receive the raw images, and somehow process them into some (very abstract, hard to understand) activations. If you think well, I could take the entire dataset, pass through the first layer, and generate a new dataset that is the result of applying the first layer to all your images:

After transforming my dataset, I could simply cut the first layer of my network:

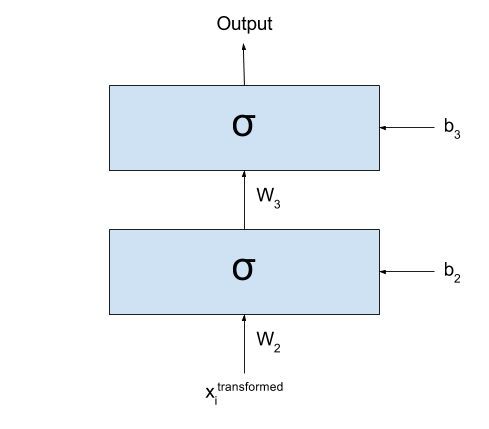
Basically what I have now is exactly the same as I had before: all my input data $\textbf{x}$ was transformed into a new dataset $\textbf{x}^{transformed}$ by going through the first layer of my network. I could even forget that my dataset one day were those images and imagine that the dataset for my classification task is actually $\textbf{x}^{transformed}$.

Well, since we are here, what prevents me from repeating this procedure again and again? As we keep doing this multiple times, we would see that the new datasets that we are generating divide the space better and better for our classification problem.

Now, there are many ways in which I can say this, so I’ll say it in all ways I can think of:

• Each new dataset is composed by “latent variables” extracted from the preceding dataset.
• Each new dataset is composed by “features” extracted from the preceding dataset.
• Each new dataset is a new “representation” extracted from the preceding dataset.

Work on learning new representations from the data is interesting because very often some representations extracted from the raw data when performing a certain task may be useful for performing several other tasks. For example, features extracted for doing image classification may be “reused” for, say, Visual Question Answering (where a model has to answer question about an image). This is a vivid area of research, with conferences every year whose sole purpose is discussing the learning of representations!

However

There is a catch on what I said.

I spent the post saying that, at each step, the layers would separate the data space better and better for the task we are performing. If that is the case, then any network with A LOT of layers would perform very well, right?

But it turns out that only in ~2006 people started managing to train several layers effectively (up to then, many believed that more layers only disturbed the training, instead of helping). Why? The problem is that these same weights that may help in separating the space into a better representation, if badly trained, may end up transforming the input into complete nonsense.

Let’s assume that some of our $W_k$ is so badly trained that, for any given input, it returns something that is completely (REALLY) random (I actually have to stop and think about how possible this might be, but for the sake of the example let’s assume that it is). When out input data crosses that one transformation, it loses all the structure it had. It loses any information, any recoverable piece of actual “usefulness”. From then on, any structure found in the following layers will not reflect the structures found in the input, and we are left hopeless. In fact, we don’t actually even need complete randomness to lose information.. If the “entropy” of the next representation is so high that too many “structures” that were present in the previous layer are transformed into noise, then recovering the information in the subsequent layers may be very hard (sometimes even impossible).

To illustrate how we can lose just some small structures of our data, I will use an example that is related to the meaning of my life: languages. Let’s imagine that there is some dialect of English that makes no difference between two sounds: h and r. So people living in this place say things like This is an a-hey of integers? or I went rome. (incidentally, this is actually not a huge stretch: Brazilians wouldn’t say the second one, but often say the first one. We sometimes really don’t make any difference between the two sounds. But well… we only learn English later, right?)

Now imagine what would happen if a person from this place spoke with another person from, say, the UK. The person from the UK can, most of the times, identify which words are being spoken based on other patterns in the data (for example, he knows that a-hey means array in the sentence above, because he can’t think of any word like a-hey that can go in that context). But what happens if he is talking about a product and the strange-dialect (say, Brazilian) person says:

(1) I hated it as soon as I bought it

Or even, without any context, something like

(2) I saw a hat in the ground

It is simply impossible to distinguish now which of the alternatives is the correct one: both options are right! This is what I mean when I say it is sometimes impossible to recover the information corrupted by some noise.

So what am I trying to say with all this discussion? My point here is that it is not just the introduction of several layers that brings better results, but also the usage of better algorithms for training those layers. This is what changed in ~2006, when some very notable researchers found a good algorithm for initializing each $W_k$ and $b_k$. (This algorithm became eventually known as Greedy Layer-Wise (Pre)Training, although some simply called it by the non-fancified name of “Unsupervised Pretraining”). It had finally become clear the problem were not multiple layers; the problem was elsewhere!

Conclusion

We went through some Representation Learning, and then discussed the importance of the training process in our networks. Somewhere along with this last discussion, we got an intuition on how noise can corrupt information. The ideas we went through here are very powerful. They are what drives my interest in Deep Learning. I hope you can find them as interesting as I do =)

I would like to thank three friends for having given me the ideas for this post (in alphabetic order to be fair):

• Ayushman Dash: who suggested me to write it.
• Bhupen Chauhan: he started the wondering about the ideas of memory and representation.
• Sidharth Sahu (I’ll add a link for him here soon): a lot of the discussion here are my thoughts about his wonderings during the conversation.